5.1. Fourier Methods¶

5.1.1. Power Spectrum Density based on Fourier Spectrum¶

This module provides Periodograms (classics, daniell, bartlett)

`Periodogram`(data[, sampling, window, NFFT, ...])	The Periodogram class provides an interface to periodogram PSDs
`DaniellPeriodogram`(data, P[, NFFT, detrend, ...])	Return Daniell’s periodogram.
`speriodogram`(x[, NFFT, detrend, sampling, ...])	Simple periodogram, but matrices accepted.
`WelchPeriodogram`(data[, NFFT, sampling])	Simple periodogram wrapper of numpy.psd function.
`speriodogram`(x[, NFFT, detrend, sampling, ...])	Simple periodogram, but matrices accepted.

Code author: Thomas Cokelaer 2011

References:	See [Marple]

Usage

You can compute a periodogram using speriodogram():

from spectrum import *
from pylab import plot
p = speriodogram(marple_data)
plot(p)

However, the output is not always easy to manipulate or plot, therefore it is advised to use the class Periodogram instead:

from spectrum import *
p = Periodogram(marple_data)
p()
p.plot()

This class will take care of the plotting and internal state of the computation. For instance, if you can change the output easily:

p.plot(sides='twosided')

class pdaniell(data, P, sampling=1.0, window='hann', NFFT=None, scale_by_freq=True, detrend=None)¶

Bases: spectrum.psd.FourierSpectrum

The pdaniell class provides an interface to DaniellPeriodogram

from spectrum import *
data = data_cosine(N=4096, sampling=4096)
p = pdaniell(data, 8, NFFT=4096)
p()
p.plot()

pdaniell Constructor

Parameters:	data (array) – input data (list or numpy.array) P (int) – number of neighbours to average over. sampling (float) – sampling frequency of the input `data`. window (str) – a tapering window. See `Window`. NFFT (int) – total length of the final data sets (padded with zero if needed; default is 4096) scale_by_freq (bool) – detrend (str) –

speriodogram(x, NFFT=None, detrend=True, sampling=1.0, scale_by_freq=True, window='hamming', axis=0)¶

Simple periodogram, but matrices accepted.

Parameters:	x – an array or matrix of data samples. NFFT – length of the data before FFT is computed (zero padding) detrend (bool) – detrend the data before co,puteing the FFT sampling (float) – sampling frequency of the input `data`. scale_by_freq – window (str) –
Returns:	2-sided PSD if complex data, 1-sided if real.

if a matrix is provided (using numpy.matrix), then a periodogram is computed for each row. The returned matrix has the same shape as the input matrix.

The mean of the input data is also removed from the data before computing the psd.

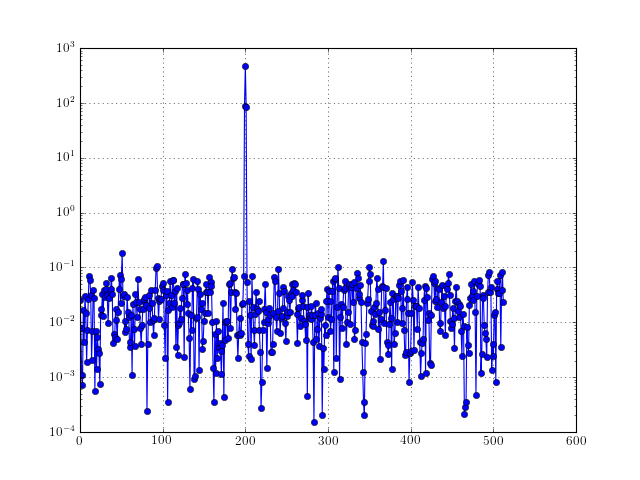
from pylab import *
from spectrum import *
data = data_cosine(N=1024, A=0.1, sampling=1024, freq=200)
semilogy(speriodogram(data, detrend=False, sampling=1024), marker='o')
grid(True)

[hires.png, pdf]

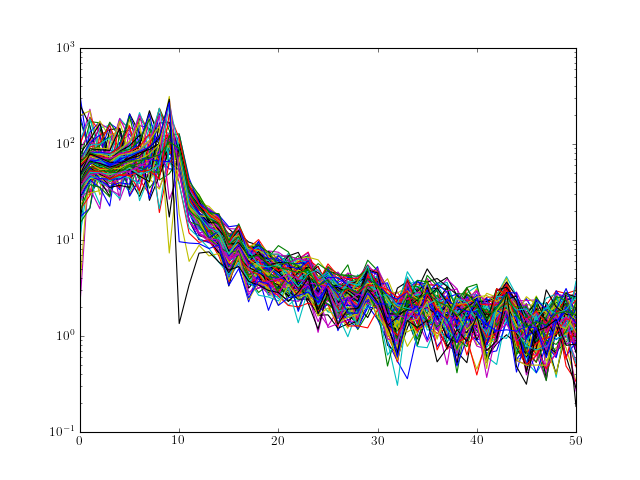
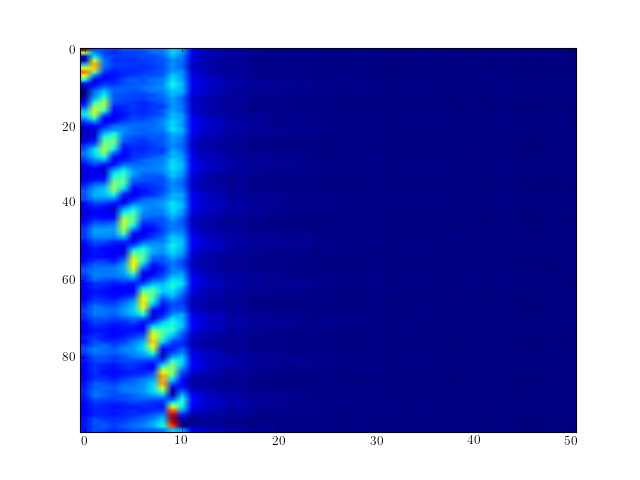
from spectrum import *
from pylab import *
# create N data sets and make the frequency dependent on the time
N = 100
m = numpy.concatenate([data_cosine(N=1024, A=0.1, sampling=1024, freq=x) for x in range(1, N)]);
m.resize(N, 1024)
res = speriodogram(m)
figure(1)
semilogy(res)
figure(2)
imshow(res.transpose(), aspect='auto')

[hires.png, pdf]

[hires.png, pdf]

Todo

a proper spectrogram class/function that takes care of normalisation

class Periodogram(data, sampling=1.0, window='hann', NFFT=None, scale_by_freq=False, detrend=None)¶

Bases: spectrum.psd.FourierSpectrum

The Periodogram class provides an interface to periodogram PSDs

from spectrum import *
data = data_cosine(N=1024, A=0.1, sampling=1024, freq=200)
p = Periodogram(data, sampling=1024)
p()
p.plot(marker='o')

[hires.png, pdf]

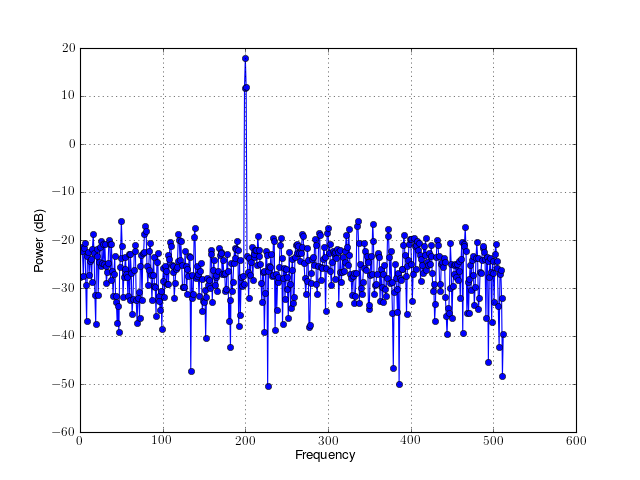
Periodogram Constructor

Parameters:	data (array) – input data (list or numpy.array) sampling (float) – sampling frequency of the input `data`. window (str) – a tapering window. See `Window`. NFFT (int) – total length of the final data sets (padded with zero if needed; default is 4096) scale_by_freq (bool) – detrend (str) –

WelchPeriodogram(data, NFFT=None, sampling=1.0, **kargs)¶

Simple periodogram wrapper of numpy.psd function.

Technical documentation:
Parameters:	A – the input data NFFT (int) – total length of the final data sets (padded with zero if needed; default is 4096) window (str) –

When we calculate the periodogram of a set of data we get an estimation of the spectral density. In fact as we use a Fourier transform and a truncated segments the spectrum is the convolution of the data with a rectangular window which Fourier transform is

$W(s)= \frac{1}{N^2} \left[ \frac{\sin(\pi s)}{\sin(\pi s/N)} \right]^2$

Thus oscillations and sidelobes appears around the main frequency. One aim of t he tapering is to reduced this effects. We multiply data by a window whose sidelobes are much smaller than the main lobe. Classical window is hanning window. But other windows are available. However we must take into account this energy and divide the spectrum by energy of taper used. Thus periodogram becomes :

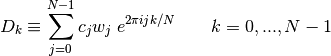
$D_k \equiv \sum_{j=0}^{N-1}c_jw_j \; e^{2\pi ijk/N} \qquad k=0,...,N-1$

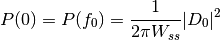
$P(0)=P(f_0)=\frac{1}{2\pi W_{ss}}\arrowvert{D_0}\arrowvert^2$

$P(f_k)=\frac{1}{2\pi W_{ss}} \left[\arrowvert{D_k}\arrowvert^2+\arrowvert{D_{N-k}}\arrowvert^2\right] \qquad k=0,1,..., \left( \frac{1}{2}-1 \right)$

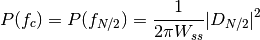
$P(f_c)=P(f_{N/2})= \frac{1}{2\pi W_{ss}} \arrowvert{D_{N/2}}\arrowvert^2$

with

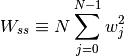
${W_{ss}} \equiv N\sum_{j=0}^{N-1}w_j^2$

from spectrum import *
psd = WelchPeriodogram(marple_data, 256)

[hires.png, pdf]

DaniellPeriodogram(data, P, NFFT=None, detrend='mean', sampling=1.0, scale_by_freq=True, window='hamming')¶

Return Daniell’s periodogram.

To reduce fast fluctuations of the spectrum one idea proposed by daniell is to average each value with points in its neighboorhood. It’s like a low filter.

$\hat{P}_D[f_i]= \frac{1}{2P+1} \sum_{n=i-P}^{i+P} \tilde{P}_{xx}[f_n]$

where P is the number of points to average.

Daniell’s periodogram is the convolution of the spectrum with a low filter:

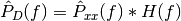
$\hat{P}_D(f)= \hat{P}_{xx}(f)*H(f)$

Example:

>>> DaniellPeriodogram(data,8)

if N/P is not integer, the final values of the original PSD are not used.

using DaniellPeriodogram(data, 0) should give the original PSD.

Correlogram PSD estimates

This module provides Correlograms methods

`CORRELOGRAMPSD`(X[, Y, lag, window, norm, ...])	PSD estimate using correlogram method.
`pcorrelogram`(data[, sampling, lag, window, ...])	The Correlogram class provides an interface to `CORRELOGRAMPSD()`.

Code author: Thomas Cokelaer 2011

References:	See [Marple]

CORRELOGRAMPSD(X, Y=None, lag=-1, window='hamming', norm='unbiased', NFFT=4096, window_params={}, correlation_method='xcorr')¶

PSD estimate using correlogram method.

Parameters:

Parameters:	X (array) – complex or real data samples X(1) to X(N) Y (array) – complex data samples Y(1) to Y(N). If provided, computes the cross PSD, otherwise the PSD is returned lag (int) – highest lag index to compute. Must be less than N window_name (str) – see `window` for list of valid names norm (str) – one of the valid normalisation of `xcorr()` (biased, unbiased, coeff, None) NFFT (int) – total length of the final data sets (padded with zero if needed; default is 4096) correlation_method (str) – either xcorr or CORRELATION. CORRELATION should be removed in the future.
Returns:	Array of real (cross) power spectral density estimate values. This is a two sided array with negative values following the positive ones whatever is the input data (real or complex).

X (array) – complex or real data samples X(1) to X(N)
Y (array) – complex data samples Y(1) to Y(N). If provided, computes the cross PSD, otherwise the PSD is returned
lag (int) – highest lag index to compute. Must be less than N
window_name (str) – see window for list of valid names
norm (str) – one of the valid normalisation of xcorr() (biased, unbiased, coeff, None)
NFFT (int) – total length of the final data sets (padded with zero if needed; default is 4096)
correlation_method (str) – either xcorr or CORRELATION. CORRELATION should be removed in the future.

Returns:

Array of real (cross) power spectral density estimate values. This is a two sided array with negative values following the positive ones whatever is the input data (real or complex).

Description:

The exact power spectral density is the Fourier transform of the autocorrelation sequence:

$P_{xx}(f) = T \sum_{m=-\infty}^{\infty} r_{xx}[m] exp^{-j2\pi fmT}$

The correlogram method of PSD estimation substitutes a finite sequence of autocorrelation estimates 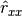$\hat{r}_{xx}$ in place of 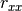$r_{xx}$ . This estimation can be computed with xcorr() or CORRELATION() by chosing a proprer lag L. The estimated PSD is then

$\hat{P}_{xx}(f) = T \sum_{m=-L}^{L} \hat{r}_{xx}[m] exp^{-j2\pi fmT}$

The lag index must be less than the number of data samples N. Ideally, it should be around L/10 [Marple] so as to avoid greater statistical variance associated with higher lags.

To reduce the leakage of the implicit rectangular window and therefore to reduce the bias in the estimate, a tapering window is normally used and lead to the so-called Blackman and Tukey correlogram:

$\hat{P}_{BT}(f) = T \sum_{m=-L}^{L} w[m] \hat{r}_{xx}[m] exp^{-j2\pi fmT}$

The correlogram for the cross power spectral estimate is

$\hat{P}_{xx}(f) = T \sum_{m=-L}^{L} \hat{r}_{xx}[m] exp^{-j2\pi fmT}$

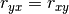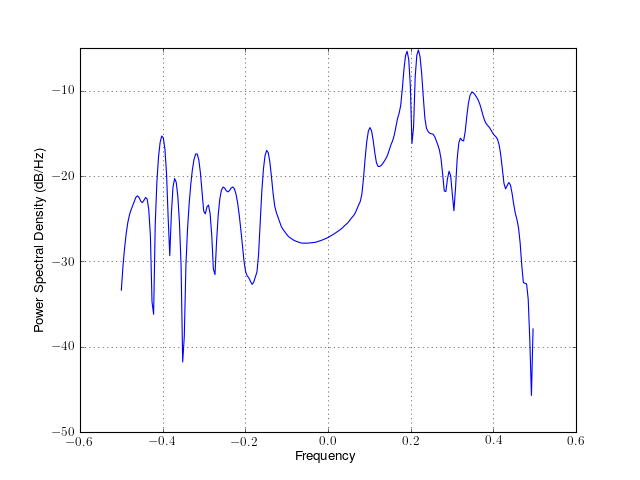
which is computed if Y is not provide. In such case, $r_{yx} = r_{xy}$ so we compute the correlation only once.

from spectrum import *
from pylab import *

psd = CORRELOGRAMPSD(marple_data, marple_data, lag=15)
f = linspace(-0.5, 0.5, len(psd))
psd = cshift(psd, len(psd)/2)
plot(f, 10*log10(psd/max(psd)))
axis([-0.5,0.5,-50,0])
grid(True)

[hires.png, pdf]

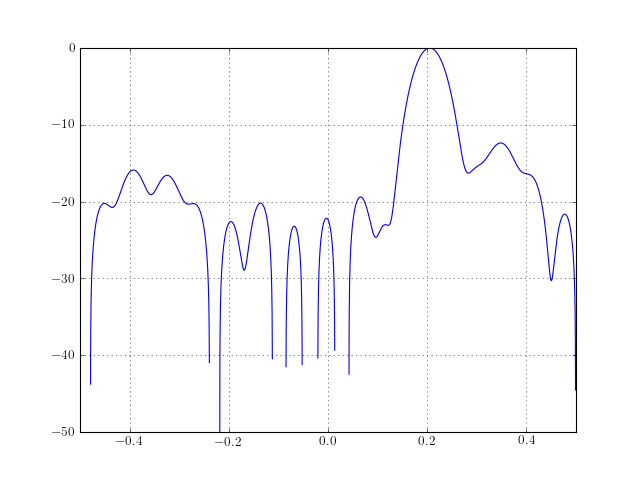
See also

create_window(), CORRELATION(), xcorr(), pcorrelogram.

class pcorrelogram(data, sampling=1.0, lag=-1, window='hamming', NFFT=None, scale_by_freq=True, detrend=None)¶

Bases: spectrum.psd.FourierSpectrum

The Correlogram class provides an interface to CORRELOGRAMPSD().

It returns an object that inherits from FourierSpectrum and therefore ease the manipulation of PSDs.

from spectrum import *
p = pcorrelogram(data_cosine(N=1024), lag=15)
p()
p.plot()
p.plot(sides='twosided')

[hires.png, pdf]

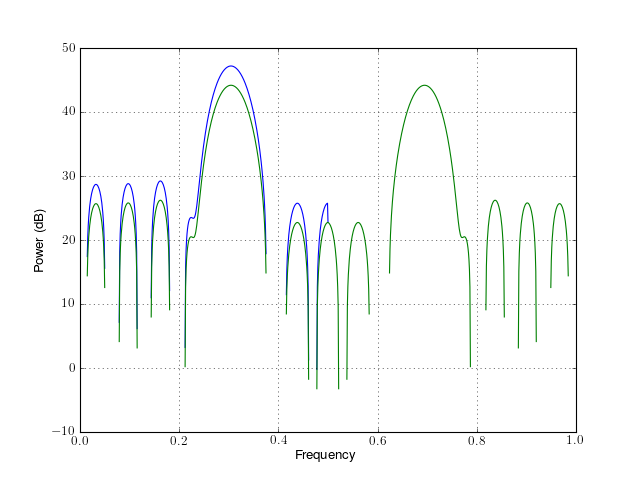
Correlogram Constructor

Parameters:	data (array) – input data (list or numpy.array) sampling (float) – sampling frequency of the input `data`. lag (int) – window (str) – a tapering window. See `Window`. NFFT (int) – total length of the final data sets (padded with zero if needed; default is 4096) scale_by_freq (bool) – detrend (str) –

5.1.2. Tapering Windows¶

This module contains tapering windows utilities.

`Window`(N[, name, norm])	Window tapering object
`window_visu`([N, name])	A Window visualisation tool
`create_window`(N[, name])	Returns the N-point window given a valid name
`window_hann`(N)	Hann window (or Hanning). (wrapping of numpy.bartlett)
`window_hamming`(N)	Hamming window
`window_bartlett`(N)	Bartlett window (wrapping of numpy.bartlett) also known as Fejer
`window_bartlett_hann`(N)	Bartlett-Hann window
`window_blackman`(N[, alpha])	Blackman window
`window_blackman_harris`(N)	Blackman Harris window
`window_blackman_nuttall`(N)	Blackman Nuttall window
`window_bohman`(N)	Bohman tapering window
`window_chebwin`(N[, attenuation])	Cheb window
`window_cosine`(N)	Cosine tapering window also known as sine window.
`window_flattop`(N[, mode, precision])	Flat-top tapering window
`window_gaussian`(N[, alpha])	Gaussian window
`window_hamming`(N)	Hamming window
`window_hann`(N)	Hann window (or Hanning). (wrapping of numpy.bartlett)
`window_kaiser`(N[, beta, method])	Kaiser window
`window_lanczos`(N)	Lanczos window also known as sinc window.
`window_nuttall`(N)	Nuttall tapering window
`window_parzen`(N)	Parsen tapering window (also known as de la Valle-Poussin)
`window_tukey`(N[, r])	Tukey tapering window (or cosine-tapered window)

Code author: Thomas Cokelaer 2011

References:	See [Nuttall], [Marple], [Harris]

class Window(N, name=None, norm=True, **kargs)¶

Window tapering object

This class provides utilities to manipulate tapering windows. Plotting functions allows to visualise the time and frequency response. It is also possible to retrieve relevant quantities such as the equivalent noise band width.

The following examples illustrates the usage. First, we create the window by providing a name and a size:

from spectrum import *
w = Window(64, 'hamming')

The window has been computed and the data is stored in:

w.data

This object contains plotting methods so that you can see the time or frequency response.

from spectrum.window import Window
w = Window(64, 'hamming')
w.plot_frequencies()

[hires.png, pdf]

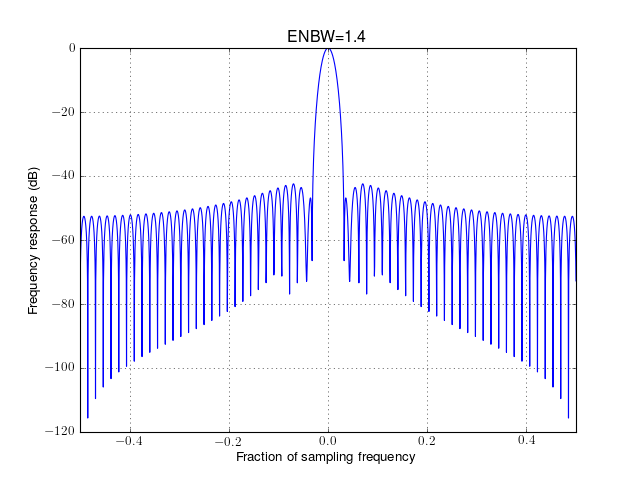
Some windows may accept optional arguments. For instance, window_blackman() accepts an optional argument called 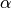$\alpha$ as well as Window. Indeed, we use the factory create_window(), which manage all the optional arguments. So you can write:

w = Window(64, 'blackman', alpha=1)

See also

create_window().

Constructor:

Create a tapering window object

Parameters:	N – the window length name – the type of window, e.g., ‘Hann’ norm – normalise the window in frequency domain (for plotting) kargs – any of `create_window()` valid optional arguments.

Attributes:

data: time series data
frequencies: getter to the frequency series
response: getter to the PSD
enbw: getter to the Equivalent noise band width.

N¶: Getter for the window length

compute_response(**kargs)¶

Compute the window data frequency response

Parameters:	norm – True by default. normalised the frequency data. NFFT (int) – total length of the final data sets( 2048 by default. if less than data length, then NFFT is set to the data length*2).

The response is stored in response.

Note

Units are dB (20 log10) since we plot the frequency response)

data¶: Getter for the window values (in time)

enbw¶: getter for the equivalent noise band width. See enbw() function

frequencies¶: Getter for the frequency array

info()¶: Print object information such as length and name

mean_square¶: returns :math:` rac{w^2}{N}`

name¶: Getter for the window name

norm¶: Getter of the normalisation flag (True by default)

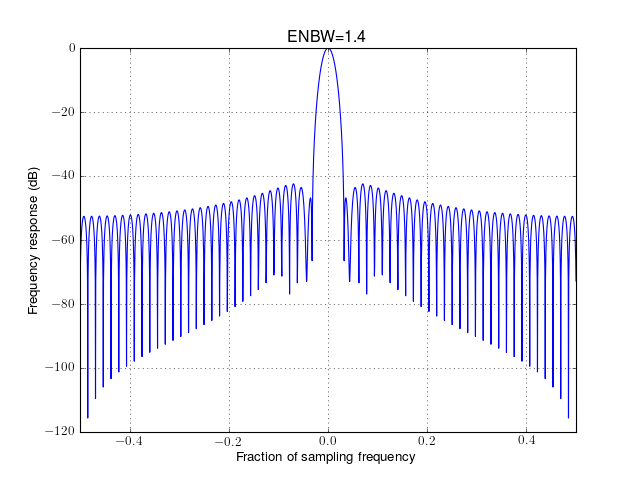
plot_frequencies(mindB=None, maxdB=None, norm=True)¶

Plot the window in the frequency domain

Parameters:	mindB – change the default lower y bound maxdB – change the default upper lower bound norm (bool) – if True, normalise the frequency response.

from spectrum.window import Window
w = Window(64, name='hamming')
w.plot_frequencies()

[hires.png, pdf]

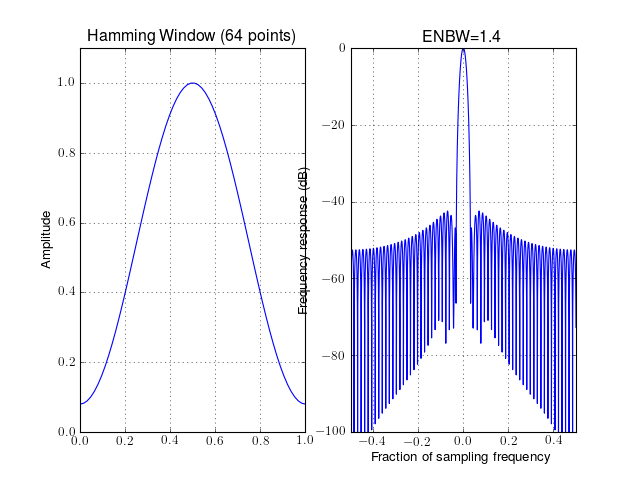
plot_time_freq(mindB=-100, maxdB=None, norm=True)¶

Plotting method to plot both time and frequency domain results.

See plot_frequencies() for the optional arguments.

from spectrum.window import Window
w = Window(64, name='hamming')
w.plot_time_freq()

[hires.png, pdf]

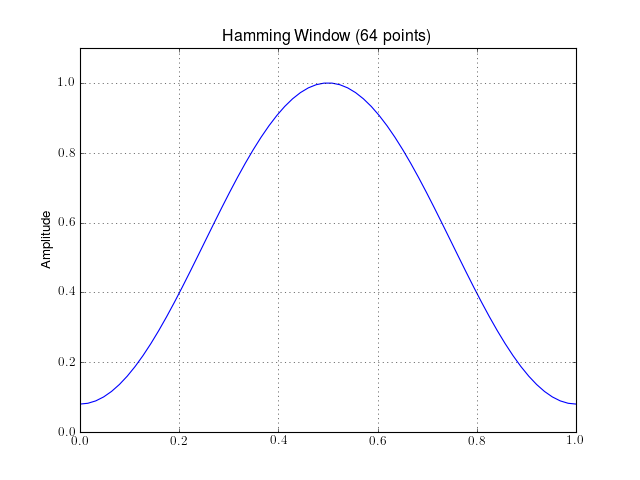
plot_window()¶

Plot the window in the time domain

from spectrum.window import Window
w = Window(64, name='hamming')
w.plot_window()

[hires.png, pdf]

response¶: Getter for the frequency response. See compute_response()

create_window(N, name=None, **kargs)¶

Returns the N-point window given a valid name

Parameters:

Parameters:	N (int) – window size name (str) – window name (default is rectangular). Valid names are stored in `window_names()`. kargs – optional arguments are: beta: argument of the `window_kaiser()` function (default is 8.6) attenuation: argument of the `window_chebwin()` function (default is 50dB) alpha: argument of the `window_gaussian()` function (default is 2.5) `window_blackman()` function (default is 0.16) `window_poisson()` function (default is 2) `window_cauchy()` function (default is 3) mode: argument `window_flattop()` function (default is symmetric, can be periodic) r: argument of the `window_tukey()` function (default is 0.5).

N (int) – window size
name (str) – window name (default is rectangular). Valid names are stored in window_names().
kargs –
optional arguments are:
- beta: argument of the window_kaiser() function (default is 8.6)
- attenuation: argument of the window_chebwin() function (default is 50dB)
- alpha: argument of the
  1. window_gaussian() function (default is 2.5)
  2. window_blackman() function (default is 0.16)
  3. window_poisson() function (default is 2)
  4. window_cauchy() function (default is 3)
- mode: argument window_flattop() function (default is symmetric, can be periodic)
- r: argument of the window_tukey() function (default is 0.5).

The following windows have been simply wrapped from existing librairies like NumPy:

Rectangular: window_rectangle(),

Bartlett or Triangular: see window_bartlett(),

Hanning or Hann: see window_hann(),

Hamming: see window_hamming(),

Kaiser: see window_kaiser(),

chebwin: see window_chebwin().

The following windows have been implemented from scratch:

Blackman: See window_blackman()

Bartlett-Hann : see window_bartlett_hann()

cosine or sine: see window_cosine()

gaussian: see window_gaussian()

Bohman: see window_bohman()

Lanczos or sinc: see window_lanczos()

Blackman Harris: see window_blackman_harris()

Blackman Nuttall: see window_blackman_nuttall()

Nuttall: see window_nuttall()

Tukey: see window_tukey()

Parzen: see window_parzen()

Flattop: see window_flattop()

Riesz: see window_riesz()

Riemann: see window_riemann()

Poisson: see window_poisson()

Poisson-Hanning: see window_poisson_hanning()

Todo

on request taylor, potter, Bessel, expo, rife-vincent, Kaiser-Bessel derived (KBD)

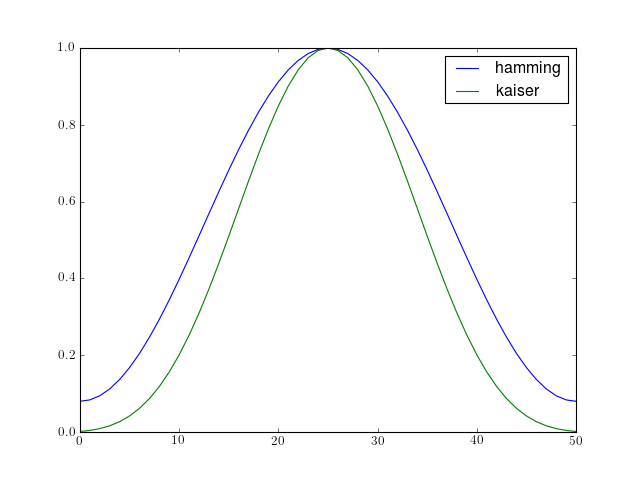
from pylab import plot, hold, legend
from spectrum import create_window

data = create_window(51, 'hamming')
plot(data, label='hamming')
hold(True)
data = create_window(51, 'kaiser')
plot(data, label='kaiser')
legend()

[hires.png, pdf]

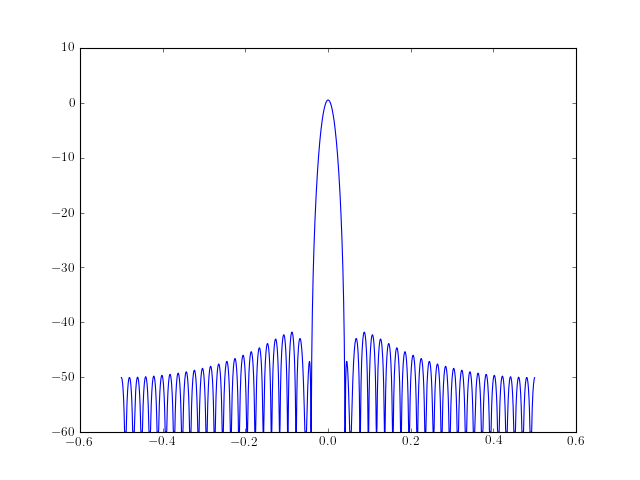
from pylab import *
from spectrum import create_window

A = fft(create_window(51, 'hamming'), 2048) / 25.5
mag = abs(fftshift(A))
freq = linspace(-0.5,0.5,len(A))
response = 20*log10(mag)
mindB = -60
response = clip(response,mindB,100)
plot(freq, response)

[hires.png, pdf]

See also

window_visu(), Window(), spectrum.dpss

enbw(data)¶

Computes the equivalent noise bandwidth

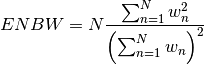
$ENBW = N \frac{\sum_{n=1}^{N} w_n^2}{\left(\sum_{n=1}^{N} w_n \right)^2}$

>>> from spectrum import *
>>> w = create_window(64, 'rectangular')

>>> enbw(w)
1.0

The following table contains the ENBW values for some of the implemented windows in this module (with N=16384). They have been double checked against litterature (Source: [Harris], [Marple]).

If not present, it means that it has not been checked.

name	ENBW	litterature
rectangular
triangle	1.3334	1.33
Hann	1.5001	1.5
Hamming	1.3629	1.36
blackman	1.7268	1.73
kaiser	1.7
blackmanharris,4	2.004
riesz	1.2000	1.2
riemann	1.32	1.3
parzen	1.917	1.92
tukey 0.25	1.102	1.1
bohman	1.7858	1.79
poisson 2	1.3130	1.3
hanningpoisson 0.5	1.609	1.61
cauchy	1.489	1.48
lanczos	1.3

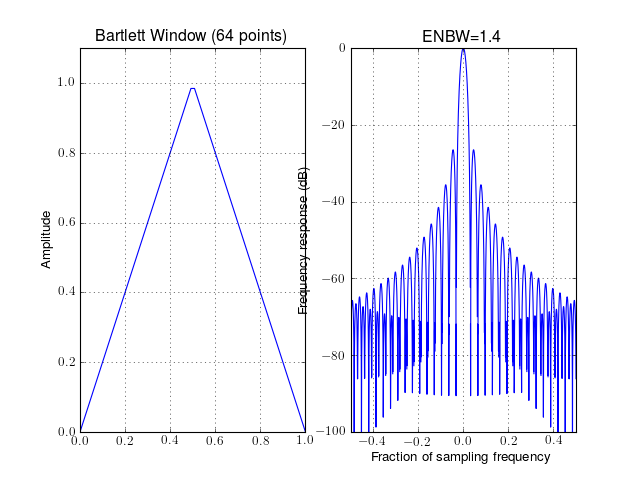
window_bartlett(N)¶

Bartlett window (wrapping of numpy.bartlett) also known as Fejer

Parameters:	N (int) – window length

The Bartlett window is defined as

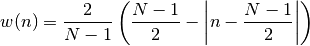
$w(n) = \frac{2}{N-1} \left( \frac{N-1}{2} - \left|n - \frac{N-1}{2}\right| \right)$

from spectrum import window_visu
window_visu(64, 'bartlett')

[hires.png, pdf]

See also

numpy.bartlett, create_window(), Window.

window_bartlett_hann(N)¶

Bartlett-Hann window

Parameters:	N – window length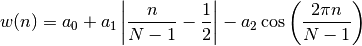

$w(n) = a_0 + a_1 \left| \frac{n}{N-1} -\frac{1}{2}\right| - a_2 \cos \left( \frac{2\pi n}{N-1} \right)$

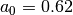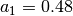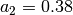
with $a_0 = 0.62$ , $a_1 = 0.48$ and $a_2=0.38$

from spectrum import window_visu
window_visu(64, 'bartlett_hann')

[hires.png, pdf]

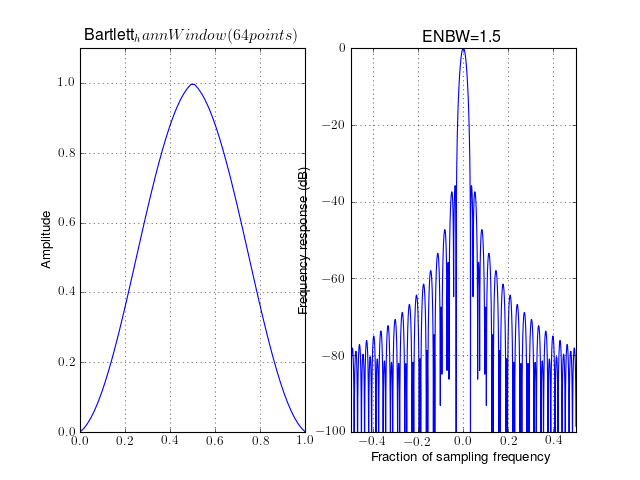
See also

create_window(), Window

window_blackman(N, alpha=0.16)¶

Blackman window

Parameters:	N – window length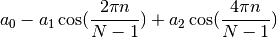

$a_0 - a_1 \cos(\frac{2\pi n}{N-1}) +a_2 \cos(\frac{4\pi n }{N-1})$

with

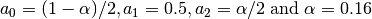
$a_0 = (1-\alpha)/2, a_1=0.5, a_2=\alpha/2 \rm{\;and\; \alpha}=0.16$

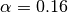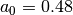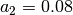When $\alpha=0.16$ , this is the unqualified Blackman window with $a_0=0.48$ and $a_2=0.08$ .

from spectrum import window_visu
window_visu(64, 'blackman')

[hires.png, pdf]

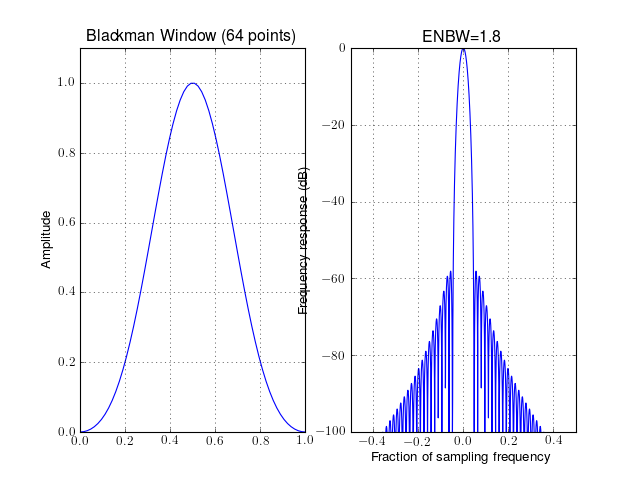
Note

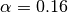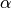Although Numpy implements a blackman window for $\alpha=0.16$ , this implementation is valid for any $\alpha$ .

See also

numpy.blackman, create_window(), Window

window_blackman_harris(N)¶

Blackman Harris window

Parameters:	N – window length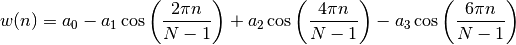

$w(n) = a_0 - a_1 \cos\left(\frac{2\pi n}{N-1}\right)+ a_2 \cos\left(\frac{4\pi n}{N-1}\right)- a_3 \cos\left(\frac{6\pi n}{N-1}\right)$

coeff	value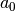
$a_0$	0.35875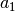
$a_1$	0.48829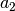
$a_2$	0.14128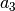
$a_3$	0.01168

from spectrum import window_visu
window_visu(64, 'blackman_harris', mindB=-80)

[hires.png, pdf]

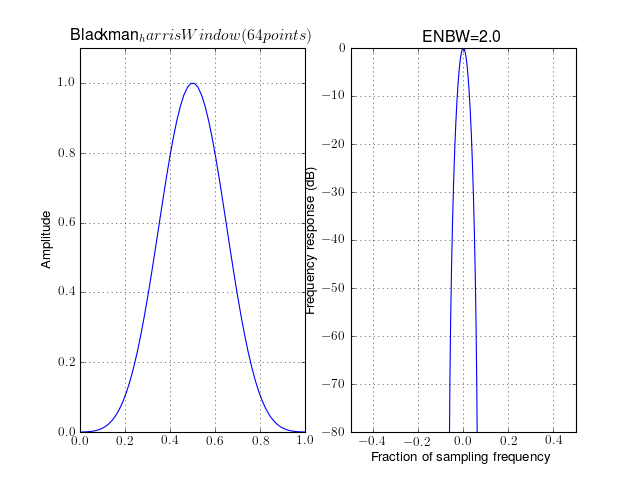
See also

spectrum.window.create_window()

See also

create_window(), Window

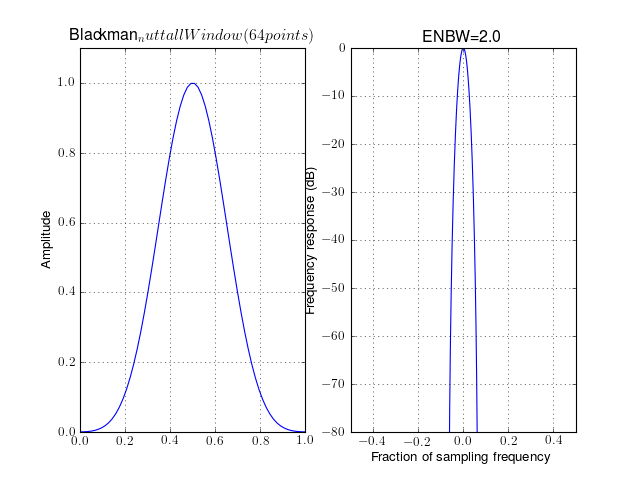
window_blackman_nuttall(N)¶

Blackman Nuttall window

returns a minimum, 4-term Blackman-Harris window. The window is minimum in the sense that its maximum sidelobes are minimized. The coefficients for this window differ from the Blackman-Harris window coefficients and produce slightly lower sidelobes.

Parameters:	N – window length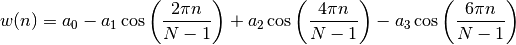

$w(n) = a_0 - a_1 \cos\left(\frac{2\pi n}{N-1}\right)+ a_2 \cos\left(\frac{4\pi n}{N-1}\right)- a_3 \cos\left(\frac{6\pi n}{N-1}\right)$

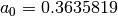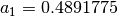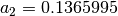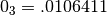
with $a_0 = 0.3635819$ , $a_1 = 0.4891775$ , $a_2=0.1365995$ and $0_3=.0106411$

from spectrum import window_visu
window_visu(64, 'blackman_nuttall', mindB=-80)

[hires.png, pdf]

See also

spectrum.window.create_window()

See also

create_window(), Window

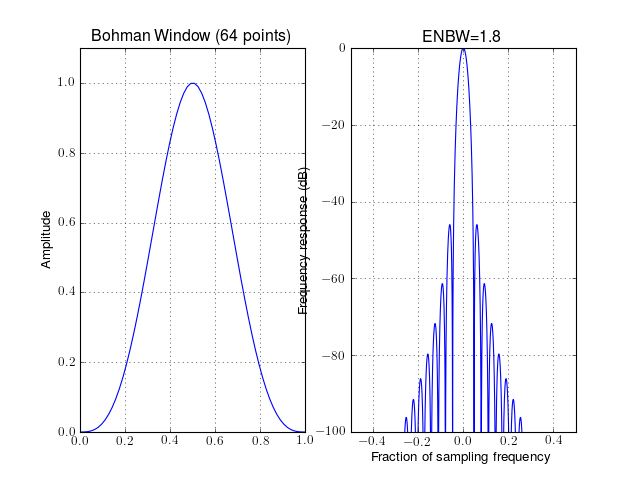
window_bohman(N)¶

Bohman tapering window

Parameters:	N – window length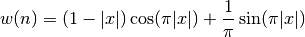

$w(n) = (1-|x|) \cos (\pi |x|) + \frac{1}{\pi} \sin(\pi |x|)$

where x is a length N vector of linearly spaced values between -1 and 1.

from spectrum import window_visu
window_visu(64, 'bohman')

[hires.png, pdf]

See also

create_window(), Window

window_cauchy(N, alpha=3)¶

Cauchy tapering window

Parameters:	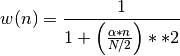N (int) – window length alpha (float) – parameter of the poisson window

$w(n) = \frac{1}{1+\left(\frac{\alpha*n}{N/2}\right)**2}$

from spectrum import window_visu
window_visu(64, 'cauchy', alpha=3)
window_visu(64, 'cauchy', alpha=4)
window_visu(64, 'cauchy', alpha=5)

[hires.png, pdf]

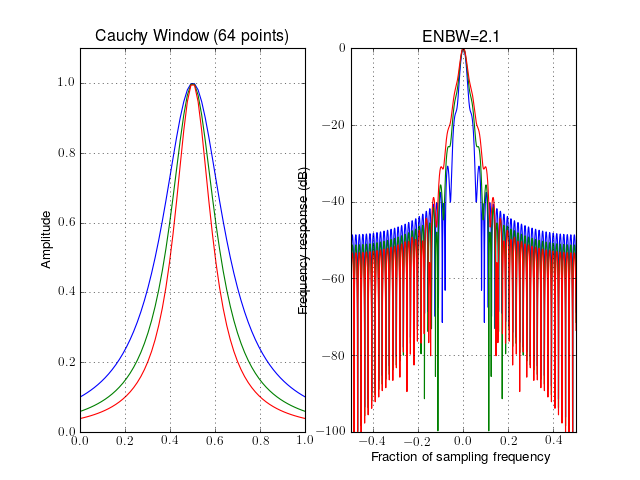
See also

window_poisson(), window_hann()

window_chebwin(N, attenuation=50)¶

Cheb window

Parameters:	N – window length

from spectrum import window_visu
window_visu(64, 'chebwin', attenuation=50)

[hires.png, pdf]

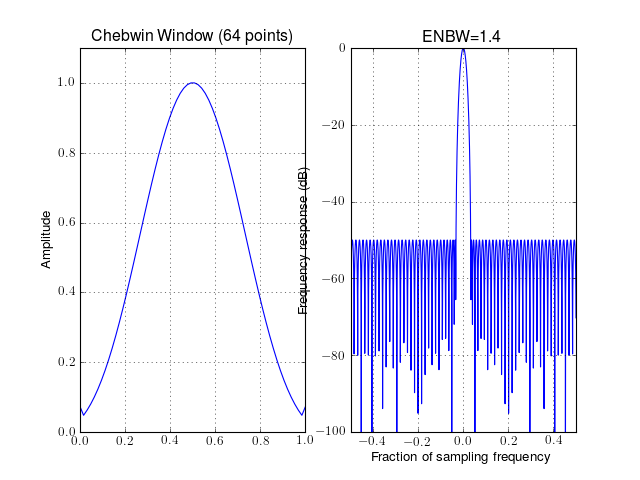
See also

scipy.signal.chebwin, create_window(), Window

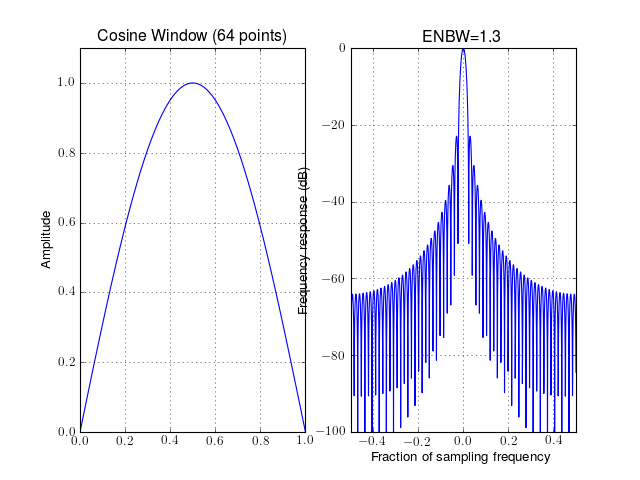
window_cosine(N)¶

Cosine tapering window also known as sine window.

Parameters:	N – window length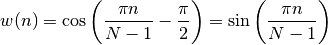

$w(n) = \cos\left(\frac{\pi n}{N-1} - \frac{\pi}{2}\right) = \sin \left(\frac{\pi n}{N-1}\right)$

from spectrum import window_visu
window_visu(64, 'cosine')

[hires.png, pdf]

See also

create_window(), Window

window_flattop(N, mode='symmetric', precision=None)¶

Flat-top tapering window

Returns symmetric or periodic flat top window.

Parameters:	N – window length mode – way the data are normalised. If mode is symmetric, then divide n by N-1. IF mode is periodic, divide by N, to be consistent with octave code.

When using windows for filter design, the symmetric mode should be used (default). When using windows for spectral analysis, the periodic mode should be used. The mathematical form of the flat-top window in the symmetric case is:

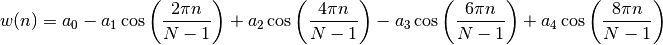
$w(n) = a_0 - a_1 \cos\left(\frac{2\pi n}{N-1}\right) + a_2 \cos\left(\frac{4\pi n}{N-1}\right) - a_3 \cos\left(\frac{6\pi n}{N-1}\right) + a_4 \cos\left(\frac{8\pi n}{N-1}\right)$

coeff	value
a0	0.21557895
a1	0.41663158
a2	0.277263158
a3	0.083578947
a4	0.006947368

from spectrum import window_visu
window_visu(64, 'bohman')

[hires.png, pdf]

See also

create_window(), Window

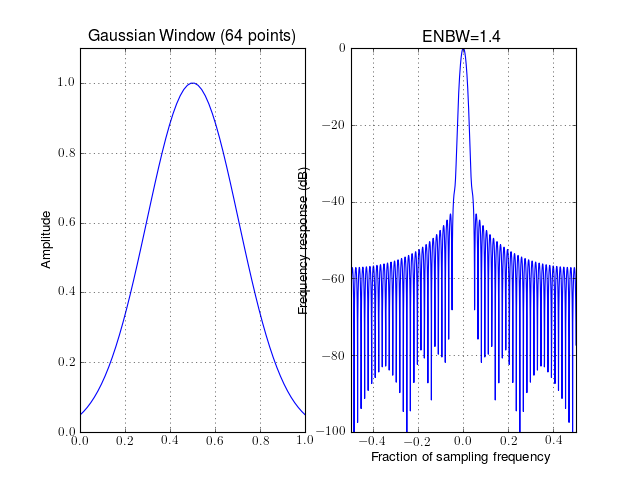
window_gaussian(N, alpha=2.5)¶

Gaussian window

Parameters:	N – window length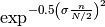

$\exp^{-0.5 \left( \sigma\frac{n}{N/2} \right)^2}$

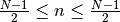with $\frac{N-1}{2}\leq n \leq \frac{N-1}{2}$ .

Note

N-1 is used to be in agreement with octave convention. The ENBW of 1.4 is also in agreement with [Harris]

from spectrum import window_visu
window_visu(64, 'gaussian', alpha=2.5)

[hires.png, pdf]

See also

scipy.signal.gaussian, create_window()

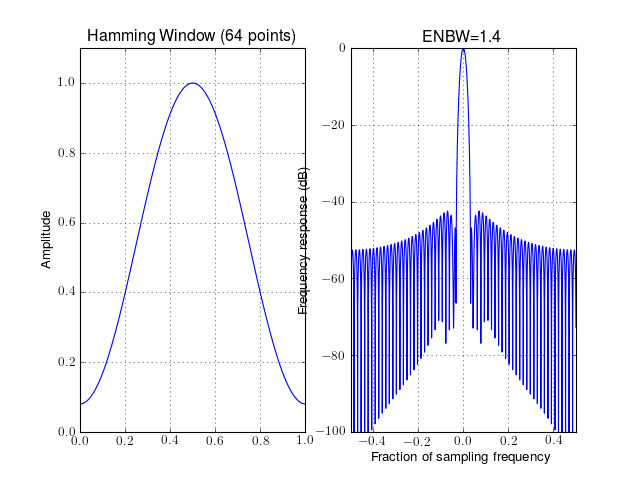
window_hamming(N)¶

Hamming window

Parameters:	N – window length

The Hamming window is defined as

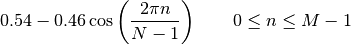
$0.54 -0.46 \cos\left(\frac{2\pi n}{N-1}\right) \qquad 0 \leq n \leq M-1$

from spectrum import window_visu
window_visu(64, 'hamming')

[hires.png, pdf]

See also

numpy.hamming, create_window(), Window.

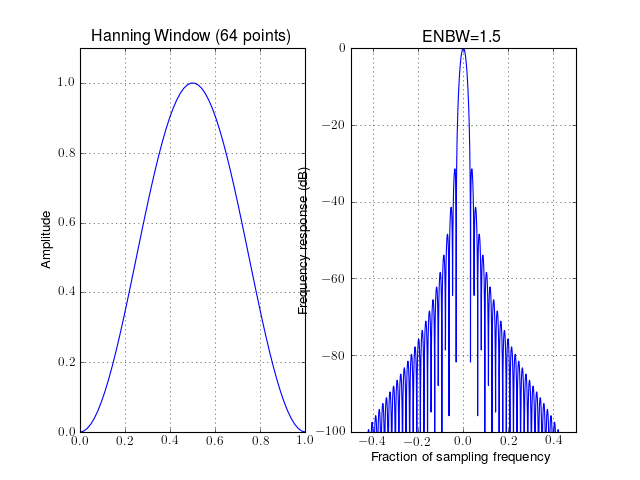
window_hann(N)¶

Hann window (or Hanning). (wrapping of numpy.bartlett)

Parameters:	N (int) – window length

The Hanning window is also known as the Cosine Bell. Usually, it is called Hann window, to avoid confusion with the Hamming window.

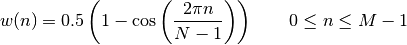
$w(n) = 0.5\left(1- \cos\left(\frac{2\pi n}{N-1}\right)\right) \qquad 0 \leq n \leq M-1$

from spectrum import window_visu
window_visu(64, 'hanning')

[hires.png, pdf]

See also

numpy.hanning, create_window(), Window.

window_kaiser(N, beta=8.6, method='numpy')¶

Kaiser window

Parameters:	N – window length beta – kaiser parameter (default is 8.6)

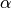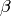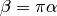To obtain a Kaiser window that designs an FIR filter with sidelobe attenuation of $\alpha$ dB, use the following $\beta$ where $\beta = \pi \alpha$ .

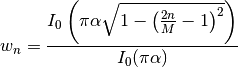
$w_n = \frac{I_0\left(\pi\alpha\sqrt{1-\left(\frac{2n}{M}-1\right)^2}\right)} {I_0(\pi \alpha)}$

where

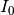$I_0$ is the zeroth order Modified Bessel function of the first kind.

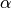$\alpha$ is a real number that determines the shape of the window. It determines the trade-off between main-lobe width and side lobe level.

the length of the sequence is N=M+1.

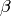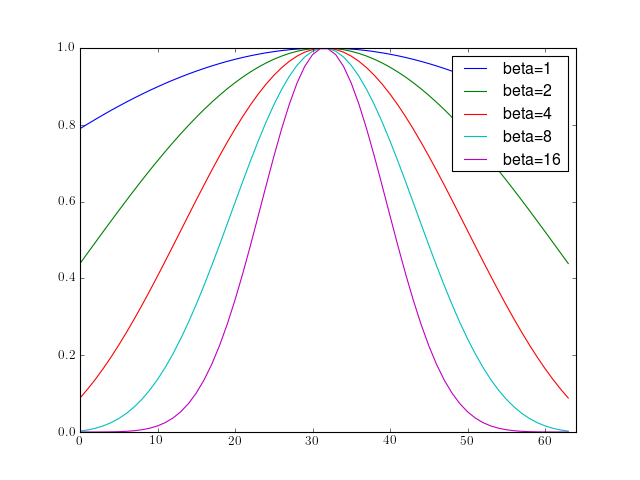
The Kaiser window can approximate many other windows by varying the $\beta$ parameter

beta	Window shape
0	Rectangular
5	Similar to a Hamming
6	Similar to a Hanning
8.6	Similar to a Blackman

from pylab import plot, legend, hold, xlim
from spectrum import window_kaiser
N = 64
for beta in [1,2,4,8,16]:
    plot(window_kaiser(N, beta), label='beta='+str(beta))
    hold(True)
xlim(0,N)
legend()

[hires.png, pdf]

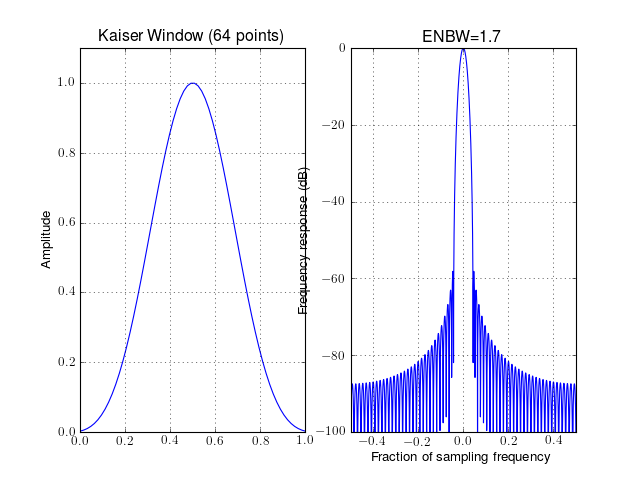
from spectrum import window_visu
window_visu(64, 'kaiser', beta=8.)

[hires.png, pdf]

window_lanczos(N)¶

Lanczos window also known as sinc window.

Parameters:	N – window length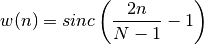

$w(n) = sinc \left( \frac{2n}{N-1} - 1 \right)$

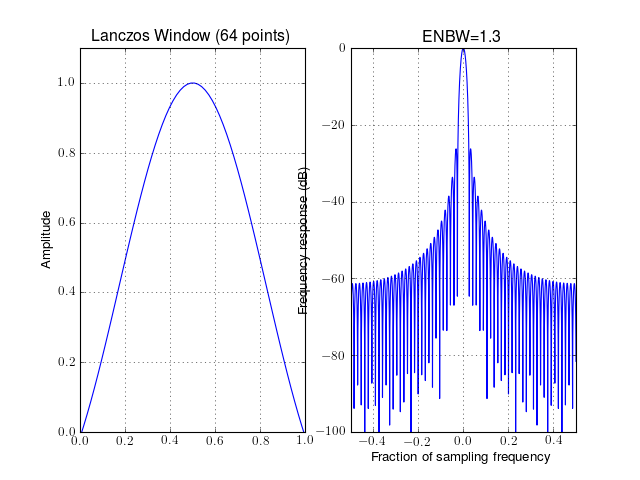
from spectrum import window_visu
window_visu(64, 'lanczos')

[hires.png, pdf]

See also

create_window(), Window

window_nuttall(N)¶

Nuttall tapering window

Parameters:	N – window length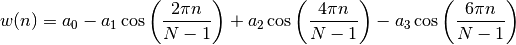

$w(n) = a_0 - a_1 \cos\left(\frac{2\pi n}{N-1}\right)+ a_2 \cos\left(\frac{4\pi n}{N-1}\right)- a_3 \cos\left(\frac{6\pi n}{N-1}\right)$

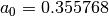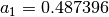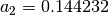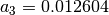
with $a_0 = 0.355768$ , $a_1 = 0.487396$ , $a_2=0.144232$ and $a_3=0.012604$

from spectrum import window_visu
window_visu(64, 'nuttall', mindB=-80)

[hires.png, pdf]

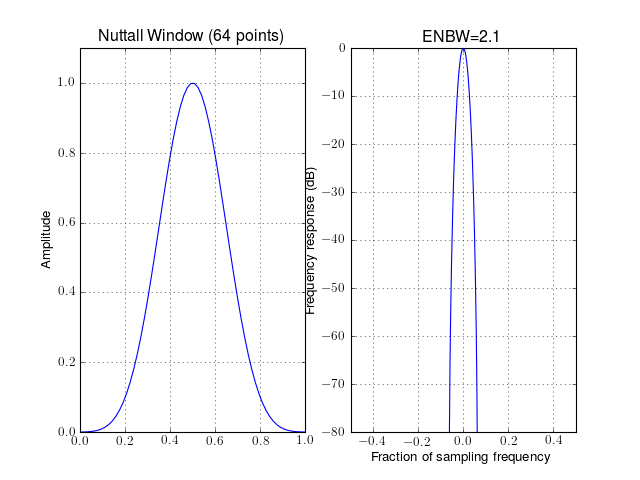
See also

create_window(), Window

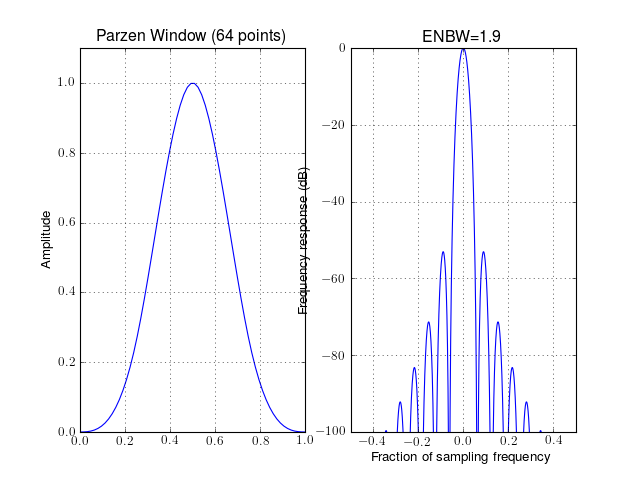
window_parzen(N)¶

Parsen tapering window (also known as de la Valle-Poussin)

Parameters:	N – window length

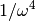Parzen windows are piecewise cubic approximations of Gaussian windows. Parzen window sidelobes fall off as $1/\omega^4$ .

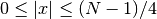if $0\leq|x|\leq (N-1)/4$ :

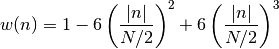
$w(n) = 1-6 \left( \frac{|n|}{N/2} \right)^2 +6 \left( \frac{|n|}{N/2}\right)^3$

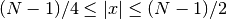
if $(N-1)/4\leq|x|\leq (N-1)/2$

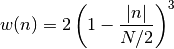
$w(n) = 2 \left(1- \frac{|n|}{N/2}\right)^3$

from spectrum import window_visu
window_visu(64, 'parzen')

[hires.png, pdf]

See also

create_window(), Window

window_poisson(N, alpha=2)¶

Poisson tapering window

Parameters:	N (int) – window length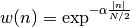

$w(n) = \exp^{-\alpha \frac{|n|}{N/2} }$

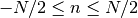with $-N/2 \leq n \leq N/2$ .

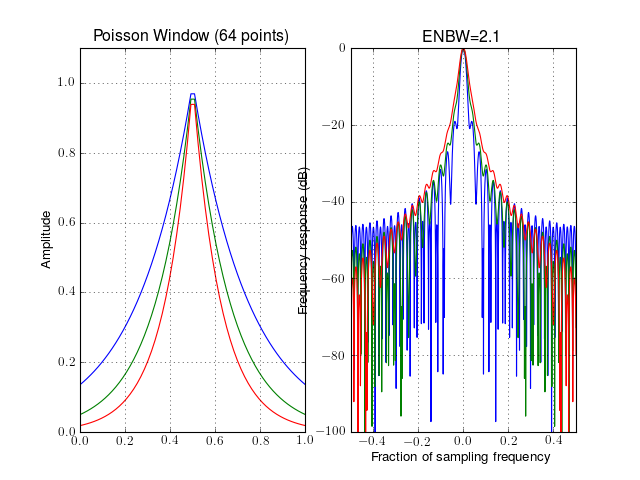
from spectrum import window_visu
window_visu(64, 'poisson')
window_visu(64, 'poisson', alpha=3)
window_visu(64, 'poisson', alpha=4)

[hires.png, pdf]

See also

create_window(), Window

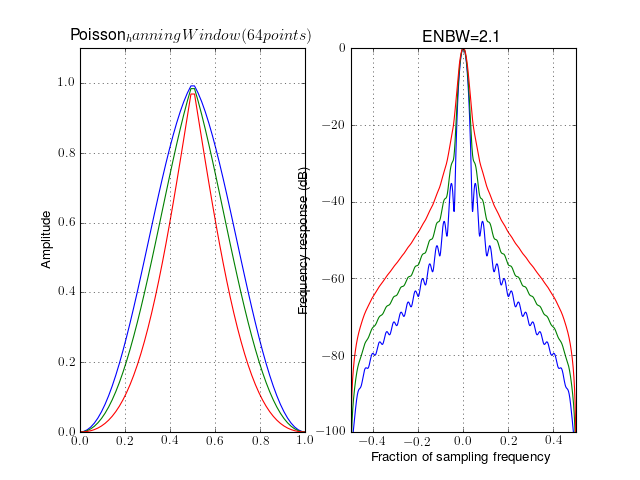
window_poisson_hanning(N, alpha=2)¶

Hann-Poisson tapering window

This window is constructed as the product of the Hanning and Poisson windows. The parameter alpha is the Poisson parameter.

Parameters:	N (int) – window length alpha (float) – parameter of the poisson window

from spectrum import window_visu
window_visu(64, 'poisson_hanning', alpha=0.5)
window_visu(64, 'poisson_hanning', alpha=1)
window_visu(64, 'poisson_hanning')

[hires.png, pdf]

See also

window_poisson(), window_hann()

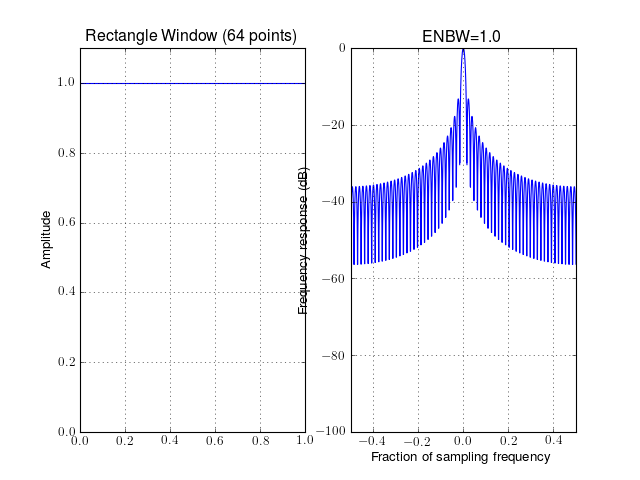
window_rectangle(N)¶

Kaiser window

Parameters:	N – window length

from spectrum import window_visu
window_visu(64, 'rectangle')

[hires.png, pdf]

window_riemann(N)¶

Riemann tapering window

Parameters:	N (int) – window length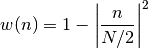

$w(n) = 1 - \left| \frac{n}{N/2} \right|^2$

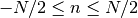with $-N/2 \leq n \leq N/2$ .

from spectrum import window_visu
window_visu(64, 'riesz')

[hires.png, pdf]

See also

create_window(), Window

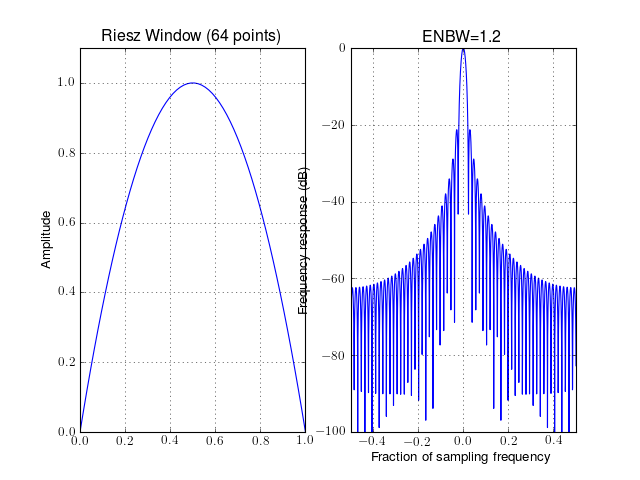
window_riesz(N)¶

Riesz tapering window

Parameters:	N – window length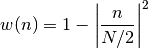

$w(n) = 1 - \left| \frac{n}{N/2} \right|^2$

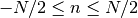with $-N/2 \leq n \leq N/2$ .

from spectrum import window_visu
window_visu(64, 'riesz')

[hires.png, pdf]

See also

create_window(), Window

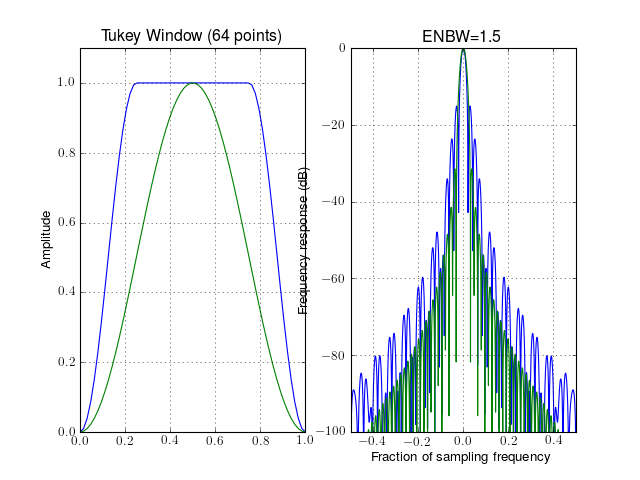
window_tukey(N, r=0.5)¶

Tukey tapering window (or cosine-tapered window)

Parameters:	N – window length r – defines the ratio between the constant section and the cosine section. It has to be between 0 and 1.

The function returns a Hanning window for r=0 and a full box for r=1.

from spectrum import window_visu
window_visu(64, 'tukey')
window_visu(64, 'tukey', r=1)

[hires.png, pdf]

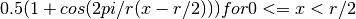
$0.5 (1+cos(2pi/r (x-r/2))) for 0<=x<r/2$

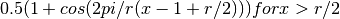
$0.5 (1+cos(2pi/r (x-1+r/2))) for x>r/2$

See also

create_window(), Window

window_visu(N=51, name='hamming', **kargs)¶

A Window visualisation tool

Parameters:	N – length of the window name – name of the window NFFT – padding used by the FFT mindB – the minimum frequency power in dB maxdB – the maximum frequency power in dB kargs – optional arguments passed to `create_window()`

This function plot the window shape and its equivalent in the Fourier domain.

from spectrum import window_visu
window_visu(64, 'kaiser', beta=8.)

[hires.png, pdf]

Front page|Spectrum - Spectral Analysis in Python (0.5.2)

5.1. Fourier Methods¶

5.1.1. Power Spectrum Density based on Fourier Spectrum¶

5.1.2. Tapering Windows¶

Search

Table Of Contents