5.3. Parametric methods¶
Contents
5.3.1. Power Spectrum Density based on Parametric Methods¶
5.3.1.1. ARMA and MA estimates (yule-walker)¶
ARMA and MA estimates, ARMA and MA PSD estimates.
ARMA model and Power Spectral Densities.
| arma_estimate | Autoregressive and moving average estimators. |
| ma | Moving average estimator. |
| arma2psd | Computes power spectral density given ARMA values. |
| parma | Class to create PSD using ARMA estimator. |
| pma | Class to create PSD using MA estimator. |
Code author: Thomas Cokelaer 2011
| References: | See [Marple] |
|---|
- arma2psd(A=None, B=None, rho=1.0, T=1.0, NFFT=4096, sides='default', norm=False)¶
Computes power spectral density given ARMA values.
This function computes the power spectral density values given the ARMA parameters of an ARMA model. It is suppose that the driving sequence is a white noise process of zero mean and variance
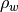 . The sampling frequency and noise variance are
used to scale the PSD output, which length is set by the user with the
NFFT parameter.
. The sampling frequency and noise variance are
used to scale the PSD output, which length is set by the user with the
NFFT parameter.Parameters: - A (array) – Array of AR parameters (complex or real)
- B (array) – Array of MA parameters (complex or real)
- rho (float) – White noise variance to scale the returned PSD
- T (float) – Sample interval in seconds to scale the returned PSD
- NFFT (int) – Final size of the PSD
- sides (str) – Default PSD is two-sided, but sides can be set to centerdc.
Warning
By convention, the AR or MA arrays does not contain the A0=1 value.
If B is None, the model is a pure AR model. If A is None, the model is a pure MA model.
Returns: two-sided PSD Details:
AR case: the power spectral density is:
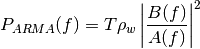
where:
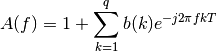
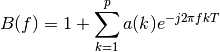
Example:
import spectrum.arma from pylab import plot, log10, hold, legend plot(10*log10(spectrum.arma.arma2psd([1,0.5],[0.5,0.5])), label='ARMA(2,2)') plot(10*log10(spectrum.arma.arma2psd([1,0.5],None)), label='AR(2)') plot(10*log10(spectrum.arma.arma2psd(None,[0.5,0.5])), label='MA(2)') legend()
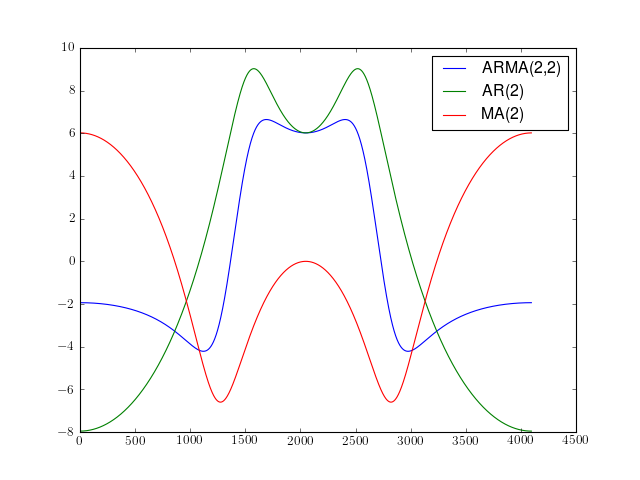
References : [Marple]
- arma_estimate(X, P, Q, lag)¶
Autoregressive and moving average estimators.
This function provides an estimate of the autoregressive parameters, the moving average parameters, and the driving white noise variance of an ARMA(P,Q) for a complex or real data sequence.
The parameters are estimated using three steps:
- Estimate the AR parameters from the original data based on a least squares modified Yule-Walker technique,
- Produce a residual time sequence by filtering the original data with a filter based on the AR parameters,
- Estimate the MA parameters from the residual time sequence.
Parameters: Returns: - A - Array of complex P AR parameter estimates
- B - Array of complex Q MA parameter estimates
- RHO - White noise variance estimate
Note
- lag must be >= Q (MA order)
from spectrum import * from pylab import * a,b, rho = arma_estimate(marple_data, 15, 15, 30) psd = arma2psd(A=a, B=b, rho=rho, sides='centerdc', norm=True) plot(10 * log10(psd)) ylim([-50,0])
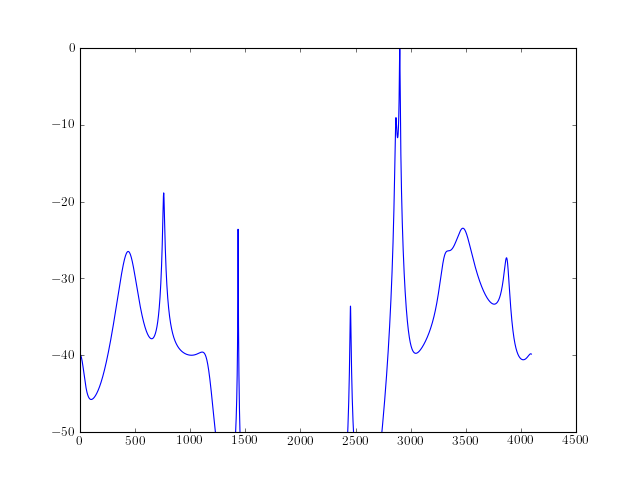
Reference : [Marple]
- ma(X, Q, M)¶
Moving average estimator.
This program provides an estimate of the moving average parameters and driving noise variance for a data sequence based on a long AR model and a least squares fit.
Parameters: Returns: - MA - Array of Q complex MA parameter estimates
- RHO - Real scalar of white noise variance estimate
from pylab import * from spectrum import * # Estimate 15 Ma parameters b, rho = ma(marple_data, 15, 30) # Create the PSD from those MA parameters psd = arma2psd(B=b, rho=rho, sides='centerdc') # and finally plot the PSD plot(linspace(-0.5, 0.5, 4096), 10 * log10(psd/max(psd))) axis([-0.5, 0.5, -30, 0])
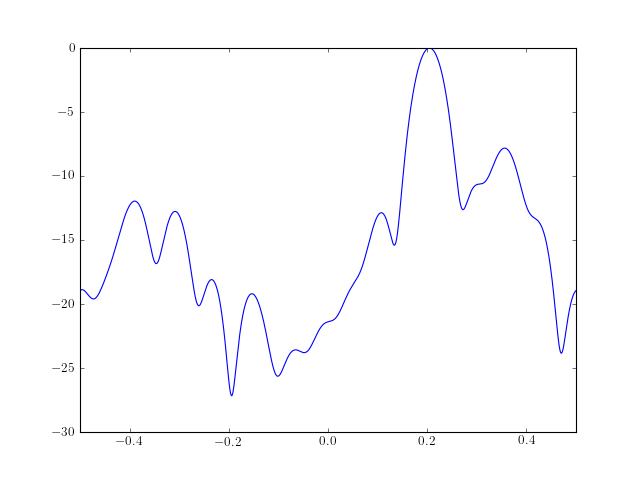
Reference : [Marple]
- class pma(data, Q, M, NFFT=None, sampling=1.0, scale_by_freq=False)¶
Class to create PSD using MA estimator.
See ma() for description.
from spectrum import * p = pma(marple_data, 15, 30, NFFT=4096) p() p.plot(sides='centerdc')
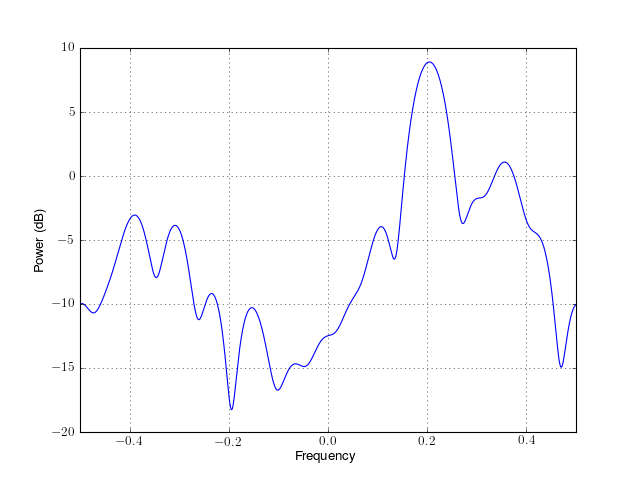
Constructor:
For a detailed description of the parameters, see ma().
Parameters:
- class parma(data, P, Q, lag, NFFT=None, sampling=1.0, scale_by_freq=False)¶
Class to create PSD using ARMA estimator.
See arma_estimate() for description.
from spectrum import * p = parma(marple_data, 4, 4, 30, NFFT=4096) p() p.plot(sides='centerdc')
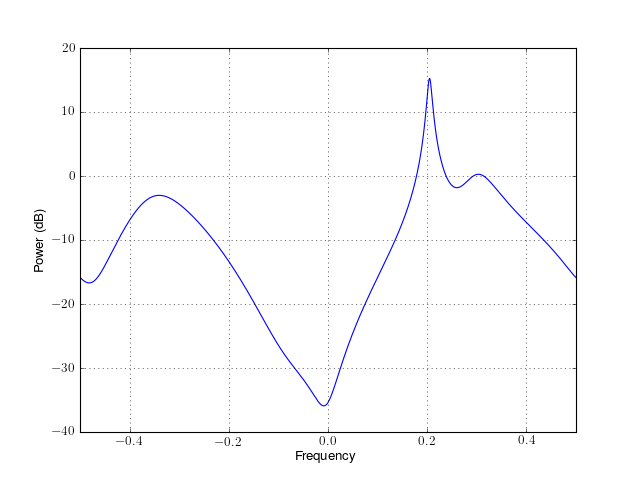
Constructor:
For a detailed description of the parameters, see arma_estimate().
Parameters:
5.3.1.2. AR estimate based on Burg algorithm¶
BURG method of AR model estimate
This module provides BURG method and BURG PSD estimate
| arburg(X, order[, criteria]) | Estimate the complex autoregressive parameters by the Burg algorithm. |
| pburg(data, order[, criteria, NFFT, sampling]) | Class to create PSD based on Burg algorithm |
Code author: Thomas Cokelaer 2011
- arburg(X, order, criteria=None)¶
Estimate the complex autoregressive parameters by the Burg algorithm.
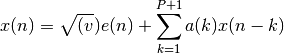
Parameters: - x – Array of complex data samples (length N)
- order – Order of autoregressive process (0<order<N)
- criteria – select a criteria to automatically select the order
Returns: - A Array of complex autoregressive parameters A(1) to A(order). First value (unity) is not included !!
- P Real variable representing driving noise variance (mean square of residual noise) from the whitening operation of the Burg filter.
- reflection coefficients defining the filter of the model.
from pylab import plot, log10, linspace, axis from spectrum import * AR, P, k = arburg(marple_data, 15) PSD = arma2psd(AR, sides='centerdc') plot(linspace(-0.5, 0.5, len(PSD)), 10*log10(PSD/max(PSD))) axis([-0.5,0.5,-60,0])
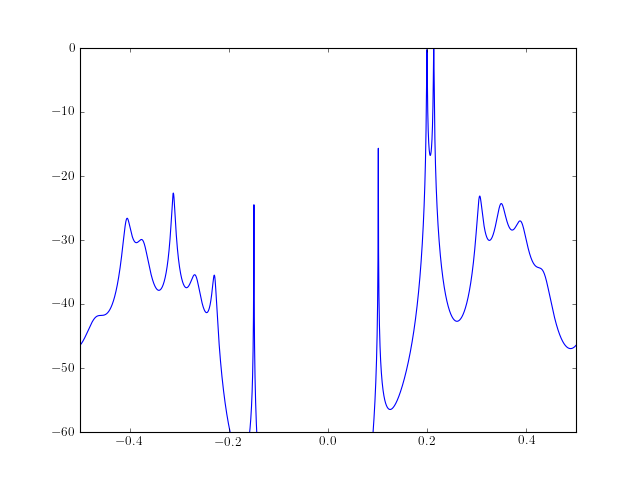
Note
- no detrend. Should remove the mean trend to get PSD. Be careful if presence of large mean.
- If you don’t know what the order value should be, choose the criterion=’AKICc’, which has the least bias and best resolution of model-selection criteria.
Note
real and complex results double-checked versus octave using complex 64 samples stored in marple_data. It does not agree with Marple fortran routine but this is due to the simplex precision of complex data in fortran.
Reference : [Marple] [octave]
- class pburg(data, order, criteria=None, NFFT=None, sampling=1.0)¶
Class to create PSD based on Burg algorithm
See arburg() for description.
from spectrum import * p = pburg(marple_data, 15, NFFT=4096) p() p.plot(sides='centerdc')
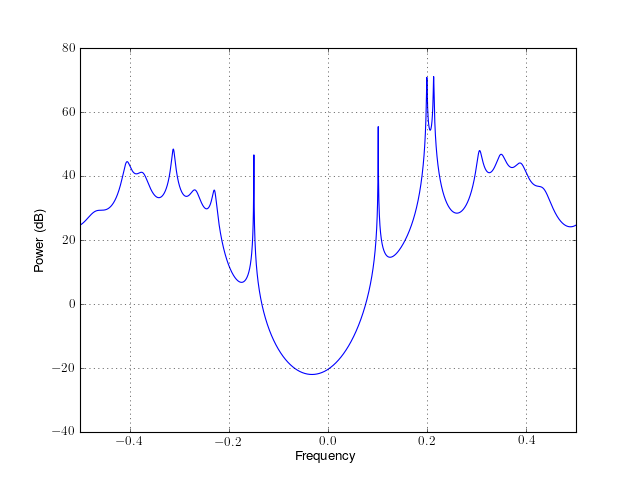
Constructor
For a detailled description of the parameters, see burg().
Parameters:
5.3.1.3. AR estimate based on YuleWalker¶
Yule Walker method to estimate AR values.
Estimation of AR values using Yule-Walker method
| aryule(X, order[, norm, allow_singularity]) | Compute AR coefficients using Yule-Walker method |
| pyule(data, order[, norm, NFFT, sampling, ...]) | Class to create PSD based on the Yule Walker method |
Code author: Thomas Cokelaer 2011
- aryule(X, order, norm='biased', allow_singularity=True)¶
Compute AR coefficients using Yule-Walker method
Parameters: Returns: - AR coefficients (complex)
- variance of white noise (Real)
- reflection coefficients for use in lattice filter
Description:
The Yule-Walker method returns the polynomial A corresponding to the AR parametric signal model estimate of vector X using the Yule-Walker (autocorrelation) method. The autocorrelation may be computed using a biased or unbiased estimation. In practice, the biased estimate of the autocorrelation is used for the unknown true autocorrelation. Indeed, an unbiased estimate may result in nonpositive-definite autocorrelation matrix. So, a biased estimate leads to a stable AR filter. The following matrix form represents the Yule-Walker equations. The are solved by means of the Levinson-Durbin recursion:
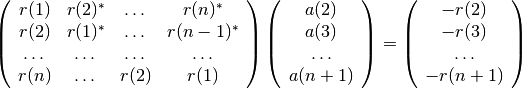
The outputs consists of the AR coefficients, the estimated variance of the white noise process, and the reflection coefficients. These outputs can be used to estimate the optimal order by using criteria.
Examples:
From a known AR process or order 4, we estimate those AR parameters using the aryule function.
>>> from scipy.signal import lfilter >>> from spectrum import * >>> from numpy.random import randn >>> A =[1, -2.7607, 3.8106, -2.6535, 0.9238] >>> noise = randn(1, 1024) >>> y = lfilter([1], A, noise); >>> #filter a white noise input to create AR(4) process >>> [ar, var, reflec] = aryule(y[0], 4) >>> # ar should contains values similar to A
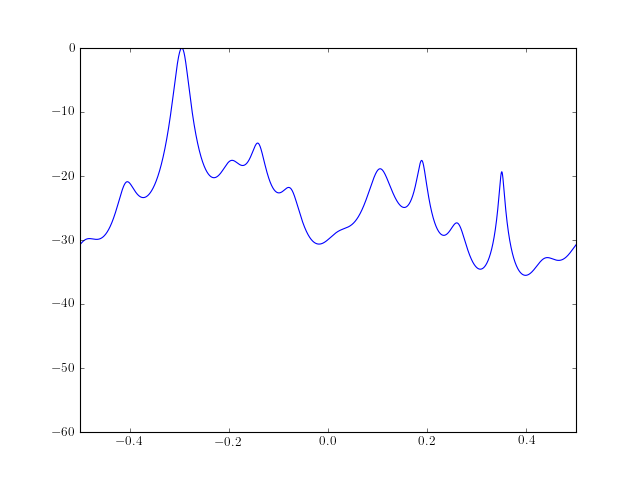
The PSD estimate of a data samples is computed and plotted as follows:
from spectrum import * from pylab import * ar, P, k = aryule(marple_data, 15, norm='biased') psd = arma2psd(ar) plot(linspace(-0.5, 0.5, 4096), 10 * log10(psd/max(psd))) axis([-0.5, 0.5, -60, 0])
Note
The outputs have been double checked against (1) octave outputs (octave has norm=’biased’ by default) and (2) Marple test code.
See also
This function uses LEVINSON() and CORRELATION(). See the criteria module for criteria to automatically select the AR order.
References : [Marple]
- class pyule(data, order, norm='biased', NFFT=None, sampling=1.0, scale_by_freq=False)¶
Class to create PSD based on the Yule Walker method
See aryule() for description.
from spectrum import * p = pyule(marple_data, 15, NFFT=4096) p() p.plot(sides='centerdc')
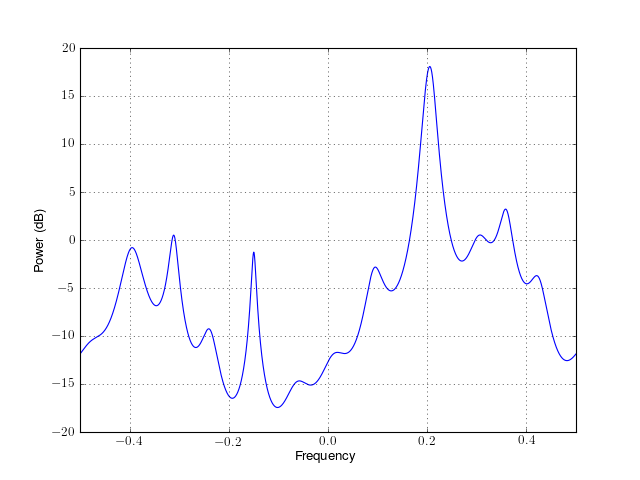
Constructor
For a detailled description of the parameters, see aryule().
Parameters:
5.3.2. Criteria¶
Criteria for parametric methods.
This module provides criteria to automatically select order in parametric PSD estimate or pseudo spectrum estimates (e.g, music).
Some criteria such as the AIC criterion helps to chose the order of PSD models such as the ARMA model. Nevertheless, it is difficult to estimate correctly the order of an ARMA model even by using these criteria. The reason being that even the Akaike criteria (AIC) does not provide the proper order with a probability of 1 with infinite samples.
The order choice is related to an expertise of the signal. There is no exact criteria. However, they may provide useful information.
AIC, AICc, KIC and AKICc are based on information theory. They attempt to balance the complexity (or length) of the model against how well the model fits the data. AIC and KIC are biased estimates of the asymmetric and the symmetric Kullback-Leibler divergence respectively. AICc and AKICc attempt to correct the bias.
There are also criteria related to eigen analysis, which takes as input the eigen values of any PSD estimate method.
Example
from spectrum import *
from pylab import *
order = arange(1, 25)
rho = [aryule(marple_data, i, norm='biased')[1] for i in order]
plot(order, AIC(len(marple_data), rho, order), label='AIC')
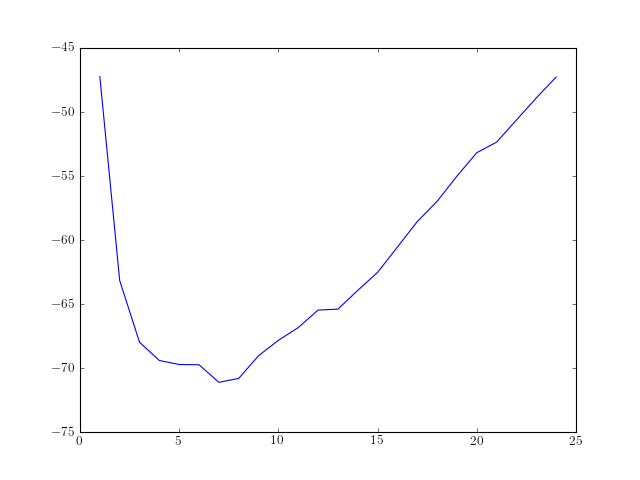
| References: | bd-Krim Seghouane and Maiza Bekara “A small sample model selection criterion based on Kullback’s symmetric divergence”, IEEE Transactions on Signal Processing, Vol. 52(12), pp 3314-3323, Dec. 2004 |
|---|
- AIC(N, rho, k)¶
Akaike Information Criterion
Parameters: - rho – rho at order k
- N – sample size
- k – AR order.
If k is the AR order and N the size of the sample, then Akaike criterion is
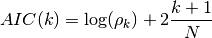
AIC(64, [0.5,0.3,0.2], [1,2,3])
Validation : double checked versus octave.
- AICc(N, rho, k, norm=True)¶
corrected Akaike information criterion
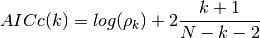
Validation : double checked versus octave.
- AKICc(N, rho, k)¶
approximate corrected Kullback information
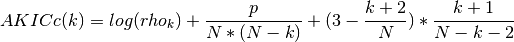
- CAT(N, rho, k)¶
Criterion Autoregressive Transfer Function :
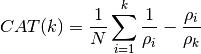
Todo
validation
- class Criteria(name, N)¶
Criteria class for an automatic selection of ARMA order.
Available criteria are
AIC see AIC() AICc see AICc() KIC see KIC() AKICc see AKICc() FPE see FPE() MDL see MDL() CAT see _CAT() Create a criteria object
Parameters: - name – a string or list of strings containing valid criteria method’s name
- N (int) – size of the data sample.
- N¶
Getter/Setter for N
- data¶
Getter/Setter for the criteria output
- error_incorrect_name = "Invalid name provided. Correct names are ['AIC', 'AICc', 'KIC', 'FPE', 'AKICc', 'MDL'] "¶
- error_no_criteria_found = "No names match the valid criteria names (['AIC', 'AICc', 'KIC', 'FPE', 'AKICc', 'MDL'])"¶
- k¶
Getter for k the order of evaluation
- name¶
Getter/Setter for the criteria name
- old_data¶
Getter/Setter for the previous value
- plot()¶
- plot_all()¶
- rho¶
Getter/Setter for rho
- valid_criteria_names = ['AIC', 'AICc', 'KIC', 'FPE', 'AKICc', 'MDL']¶
- FPE(N, rho, k=None)¶
Final prediction error criterion
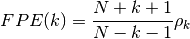
Validation : double checked versus octave.
- KIC(N, rho, k)¶
Kullback information criterion
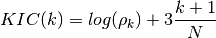
Validation : double checked versus octave.
- MDL(N, rho, k)¶
Minimum Description Length
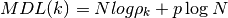
Validation : results
- aic_eigen(s, N)¶
AIC order-selection using eigen values
Parameters: - s – a list of p sorted eigen values
- N – the size of the input data. To be defined precisely.
Returns: - an array containing the AIC values
Given
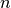 sorted eigen values
sorted eigen values 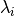 with
with
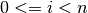 , the proposed criterion from Wax and Kailath (1985)
is:
, the proposed criterion from Wax and Kailath (1985)
is: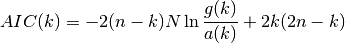
where the arithmetic sum
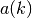 is:
is: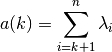
and the geometric sum
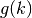 is:
is: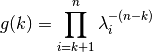
The number of relevant sinusoids in the signal subspace is determined by selecting the minimum of AIC.
See also
eigen()
Todo
define precisely the input parameter N. Should be the input data length but when using correlation matrix (SVD), I suspect it should be the length of the correlation matrix rather than the original data.
References :
- mdl_eigen(s, N)¶
MDL order-selection using eigen values
Parameters: - s – a list of p sorted eigen values
- N – the size of the input data. To be defined precisely.
Returns: - an array containing the AIC values
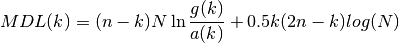
See also
aic_eigen() for details
References :